cada par de vértices en la gráfica ponderada.
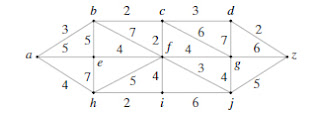
1. a, f
2. a, g
3. a, z
4. b, j
5. h, d
6. Escriba un algoritmo que encuentre la longitud de una ruta más
corta entre dos vértices dados en una gráfica conexa ponderada y
también encuentre una ruta más corta.
7. Escriba un algoritmo que encuentre las longitudes de las rutas más
cortas de un vértice dado a todos los demás vértices en una gráfica
G conexa ponderada.
8. Escriba un algoritmo que encuentre las longitudes de las rutas más
cortas entre todos los pares de vértices en una gráfica conexa ponderada
simple que tiene n vértices con tiempo O(n3).
9. Modifique el algoritmo 8.4.1 para que acepte una gráfica ponderada
que no necesariamente sea conexa. Al terminar, ¿qué es L(z)
si no hay trayectoria de a a z?
10. ¿Falso o verdadero? Cuando una gráfica conexa ponderada y los
vértices a y z son la entrada al siguiente algoritmo, regresa la longitud
de una ruta más corta de a a z. Si el algoritmo es correcto,
pruébelo; de otra manera, dé un ejemplo de una gráfica conexa
ponderada y vértices a y z para los que falla.
Algoritmo 8.4.6
algor(w, a, z) {
longitud = 0
v = a
T = conjunto de todos los vértices
while(v ¬ = z) {
T = T − {v}
seleccionar x ∈ T con w(v, x) mínimo
longitud = longitud + w(v, x)
v = x
}
return longitud
}
11. ¿Falso o verdadero? El algoritmo 8.4.1 encuentra la longitud de
una ruta más corta en una gráfica conexa ponderada incluso si algunos
pesos son negativos. Si es verdadero, pruébelo; de otra manera,
proporcione un contraejemplo.