Get 1.7.1 exercise solution
Get 1.7.2 exercise solution
Get 1.7.3 exercise solution
Get 1.7.4 exercise solution
Get 1.7.5 exercise solution
Get 1.7.6 exercise solution
Get 1.7.7 exercise solution
Get 1.7.8 exercise solution
Get 1.7.9 exercise solution
Get 1.7.10 exercise solution
Get 1.7.11 exercise solution
En los ejercicios 12 al 17, use inducción para verificar la desigualdad.
Get 1.7.12 exercise solution
Get 1.7.13 exercise solution
Get 1.7.14 exercise solution
Get 1.7.15 exercise solution
para toda n ≥ 1 y 0 < r < 1. Sugerencia: Use el resultado del ejercicio anterior, compare la suma de los términos en
en la diagonal ( ) con la suma de los términos por columna.
Get 1.7.16 exercise solution
Get 1.7.17 exercise solution
Get 1.7.18 exercise solution
Get 1.7.19 exercise solution
20. Pruebe que
para toda n ≥ 1.
En los ejercicios 21 al 24, use la inducción para probar la afirmación. Get 1.7.20 exercise solution
21. 7n − 1 es divisible entre 6, para toda n ≥ 1. Get 1.7.21 exercise solution
22. 11n − 6 es divisible entre 5, para toda n ≥ 1. Get 1.7.22 exercise solution
23. 6·7n – 2·3n es divisible entre 4, para toda n ≥ 1. Get 1.7.23 exercise solution
24. 3n + 7n – 2 es divisible entre 8, para toda n ≥ 1. Get 1.7.24 exercise solution
25. Experimentando con valores pequeños de n, adivine una fórmula para la suma
después use inducción para verificar su fórmula. Get 1.7.25 exercise solution
27. Demuestre que las regiones del ejercicio anterior pueden colorearse de rojo y verde de modo que no haya dos regiones que comparten una orilla que sean del mismo color. Get 1.7.27 exercise solution
28. Dados n ceros y n unos distribuidos de cualquier manera alrededor de un círculo (vea la figura siguiente), demuestre, por inducción sobre n, que es posible comenzar en algún número y proceder en el sentido de las manecillas del reloj alrededor del círculo hasta la posición original de inicio, de manera que en cualquier punto durante el ciclo se hayan visto al menos la misma cantidad de ceros que de unos. En la siguiente figura, un punto de inicio posible está marcado con una flecha.
30. Demuestre un tablero deficiente de 5 × 5 que es imposible enlosar con trominos. Explique por qué no se puede enlosar. Get 1.7.30 exercise solution
31. Demuestre que cualquier tablero de (2i) × (3j), donde i y j son enteros positivos, sin cuadro faltante, se puede enlosar con trominos. Get 1.7.31 exercise solution
32. Demuestre que cualquier tablero deficiente de 7 × 7 se puede enlosar con trominos. Get 1.7.32 exercise solution
33. Demuestre que cualquier tablero deficiente de 11 × 11 se puede enlosar con trominos. Sugerencia: Subdivida el tablero en tableros que se traslapan de 7 × 7 y 5 × 5 y dos tableros de 6 × 4. Después
remítase a los ejercicios 29, 31 y 32. Get 1.7.33 exercise solution
34. Este ejercicio y el siguiente se deben a Anthony Quass. Una forma- L de 2n × 2n, n ≥ 0 es una figura de la forma
sin cuadros faltantes. Demuestre que cualquier forma-L de 2n × 2n se puede enlosar con trominos. Get 1.7.34 exercise solution
35. Use el ejercicio anterior para dar una prueba diferente de que cualquier tablero deficiente de 2n × 2n se puede enlosar con trominos.
Un tromino recto es un objeto hecho de tres cuadros en fila:
Get 1.7.35 exercise solution
36. ¿Qué tableros deficientes de 4 × 4 se pueden enlosar con trominos rectos? Sugerencia: Numere los cuadros del tablero de 4 × 4, de izquierda a derecha y de arriba abajo: 1, 2, 3, 1, 2, 3, etcétera. Observe que si existe un enlosado, cada tromino recto cubre exactamente un 2 y exactamente un 3. Get 1.7.36 exercise solution
37. ¿Qué tableros deficientes de 5 × 5 se pueden enlosar con trominos rectos? Get 1.7.37 exercise solution
38. ¿Qué tableros deficientes de 8 × 8 se pueden enlosar con trominos rectos? Get 1.7.38 exercise solution
39. Use un ciclo invariante para probar que cuando el seudocódigo
i=1
pow=1
while(i ≤ n){
pow = pow * a
i=i+1
}
termina, pow es igual a an. Get 1.7.39 exercise solution
40. Pruebe que, después de que termina el siguiente seudocódigo, a[h] = val; para toda p, i ≤ p < h, a[p] < val; y para toda p, h < p ≤ j, a[p] ≥ val. En particular, val está en la posición en el arreglo
a[i], . . . , a[j] donde estaría si el arreglo fuera ordenado.
val = a[i ]
h = i
for k = i + 1 to j
if (a[k] < val) {
h = h + 1
swap(a[h], a[k])
}
swap(a[i ], a[h])
Sugerencia: Use el ciclo invariante: para toda p, i < p ≤ h, a[p] < val; y para toda p, h < p < k, a[p] ≥ val. (Un dibujo ayuda).
Esta técnica se llama particionar. Esta versión particular se debe a Nico Lomuto. Las particiones se emplean para encontrar el k-ésimo, elemento más pequeño en cualquier arreglo y para construir un algoritmo para ordenar llamado quicksort.
Un septomino en 3D es un cubo de tres dimensiones de 2 × 2 × 2 sin una esquina de 1 × 1 × 1. Un cubo deficiente es un cubo de k × k × k sin un cubo de 1 × 1 × 1. Get 1.7.40 exercise solution
41. Pruebe que un cubo deficiente de 2n × 2n × 2n se puede enlosar con septominos en 3D. Get 1.7.41 exercise solution
42. Demuestre que si un cubo deficiente de k × k × k se puede enlosar con septominos en 3D, entonces 7 divide uno de los k−1, k−2, k−4. Get 1.7.42 exercise solution
43. Suponga que Sn
= (n + 2)(n – 1) se propone (incorrectamente) como
fórmula para
2 + 4 + . . . + 2n.
a) Demuestre que el paso inductivo se satisface pero que el paso
base falla.
★ b) Si Sn
es una expresión arbitraria que satisface el paso inductivo, ¿qué forma debe tener Sn ? Get 1.7.43 exercise solution
44. ¿Qué está mal en el siguiente argumento, que se supone que prueba que cualesquiera dos enteros positivos son iguales?
Se usa inducción sobre n para “probar” que si a y b son enteros positivos y n = máx{a, b}, entonces a= b.
Paso base (n = 1). Si a y b son enteros positivos y 1 = máx{a, b}, debe tenerse a = b = 1.
Paso inductivo Suponga que si a y b son enteros positivos y n= máx{a , b }, entonces a = b . Suponga que a y b son enteros positivos y que n + 1 = máx{a, b}. Ahora n = máx{a–1, b–1}.
Por la hipótesis inductiva, a–1 = b–1. Por lo tanto, a = b.
Como se verificaron el paso base y el paso inductivo, por el principio de inducción matemática, ¡cualesquiera dos enteros positivos son iguales! Get 1.7.44 exercise solution
45. ¿Qué está mal en la siguiente “prueba” de que
para toda n ≥ 2. Esta desigualdad da una prueba correcta de la afirmación del ejercicio anterior.
En los ejercicios 47 al 51, suponga que n > 1 personas se colocan en un campo (plano euclidiano) de manera que cada una tiene un vecino más cercano único. Aún más, suponga que cada persona tiene un pastel que lanza a su vecino más cercano. Un sobreviviente es una persona a la que no le pega un pastel.
Get 1.7.45 exercise solution
Get 1.7.46 exercise solution
47. Proporcione un ejemplo para mostrar que si n es par, puede no haber un sobreviviente. Get 1.7.47 exercise solution
48. Dé un ejemplo para demostrar que puede haber más de un sobreviviente. Get 1.7.48 exercise solution
49. [Carmony] Use inducción sobre n para demostrar que si n es impar, siempre habrá al menos un sobreviviente. Get 1.7.49 exercise solution
50. Pruebe o desapruebe: Si n es impar, una de las dos personas más separadas es un sobreviviente. Get 1.7.50 exercise solution
51. Pruebe o desapruebe: Si n es impar, la persona que lanza un pastel la mayor distancia es un sobreviviente.
Los ejercicios 52 al 55 manejan conjuntos convexos planos. Un conjunto convexo plano, en adelante abreviado “conjunto convexo”, es un conjunto no vacío X en el plano que tiene la propiedad de que si x y y son cualesquiera dos puntos en X, el segmento de recta de x a y también está en X. Las siguientes figuras ilustran esto.
Get 1.7.51 exercise solution
52. Pruebe que si X y Y son conjuntos convexos y X ∩ Y (los puntos comunes a X y Y) es no vacío, X ∩ Y es un conjunto convexo. Get 1.7.52 exercise solution
53. Suponga que X1, X2, X3, X4 son conjuntos convexos, cada tres de los cuales tienen un punto en común. Pruebe que los cuatro tienen un punto en común. Get 1.7.53 exercise solution
54. Pruebe el Teorema de Helly: Suponga que X1, X2, . . . , Xn, n ≥ 4, son conjuntos convexos, cada tres de los cuales tienen un punto en común. Pruebe que los n conjuntos tienen un punto en común. Get 1.7.54 exercise solution
55. Suponga que n ≥ 3 puntos en el plano tienen la propiedad de que cada tres de ellos están contenidos en un círculo de radio 1. Pruebe que existe un círculo de radio 1 que contiene a todos los puntos. Get 1.7.55 exercise solution
56. Si a y b son números reales con a < b, un intervalo abierto (a, b) es el conjunto de números reales x tales que a < x < b. Pruebe que si I1, . . . , In es un conjunto de n ≥ 2 intervalos abiertos tales que
cada par tiene una intersección no vacía, entonces
I1 ∩ I2 ∩ · · · ∩ In
(los puntos comunes a I1, . . . , In) es no vacío.
Flavius Josephus era un soldado e historiador judío que vivió en el siglo I (vea [Graham, 1994; Schumer]). Era uno de los líderes de una revuelta judía contra Roma en el año 66. El siguiente año, se encontraba entre un grupo de soldados atrapados que decidieron suicidarse antes de que los capturaran. Una versión de la historia dice que, antes que ser capturados, formaron un círculo y procedieron a matar a cada tercera persona alrededor del círculo. Josephus, que tenía conocimientos
de matemáticas discretas, se dio cuenta dónde debían pararse él y un amigo para evitar que los mataran.
Los ejercicios 57 al 63 se refieren a una variante del problema de Josephus en el que se elimina a una persona cada dos. Se supone que n personas se colocan en un círculo y se numeran 1, 2, . . . , n en el
sentido de las manecillas del reloj. Se elimina 2, se elimina 4, etcétera, hasta que hay un sobreviviente, denotado por J(n). Get 1.7.56 exercise solution
57. Calcule J(4). Get 1.7.57 exercise solution
58. Calcule J(6). Get 1.7.58 exercise solution
59. Calcule J(10). Get 1.7.59 exercise solution
60. Use la inducción para demostrar que J(2i) = 1 para toda i ≥ 1. Get 1.7.60 exercise solution
61. Con un valor de n ≥ 2, sea 2i la potencia más grande de 2 tal que 2i ≤ n. (Ejemplos: Si n = 10, i = 3. Si n = 16, i = 4.) Sea j = n – 2i. (Después de restar de n, 2i, la potencia más grande de 2 menor
o igual que n, j es lo que queda.) Usando el resultado del ejerejercicio 60 o de otra manera, pruebe que J(n) = 2j + 1. Get 1.7.61 exercise solution
62. Use el resultado del ejercicio 61 para calcular J(1000). Get 1.7.62 exercise solution
63. Use el resultado del ejercicio 61 para calcular J (100,000).
Si a1, a2, . . . es una secuencia, se define el operador diferencia Δ como
an = an+1 − an. Get 1.7.63 exercise solution
La fórmula del ejercicio 64 se utiliza en ocasiones para encontrar una fórmula para una suma en lugar de usar la inducción para probar una fórmula para la suma (vea los ejercicios 65 al 67).
La fórmula del ejercicio 64 se utiliza en ocasiones para encontrar una fórmula para una suma en lugar de usar la inducción para probar una fórmula para la suma (vea los ejercicios 65 al 67).
64. Suponga que Δan = bn. Demuestre que
b1 + b2 +· · ·+bn = an+1 − a1.
Esta fórmula es análoga a la fórmula de cálculo
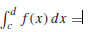g(d)−g(c),donde Dg = f (D es el operador derivada). En la fórmula de cálculo, la suma se sustituye por la integral y Δ se sustituye por la derivada. Get 1.7.64 exercise solution
65. Sea an = n2, calcule Δan. Use el ejercicio 64 para encontrar una fórmula para 1 + 2 + 3 +. . .+n. Get 1.7.65 exercise solution
66. Use el ejercicio 64 par encontrar una fórmula para
1(1!) + 2(2!) +· · ·+n(n!).
(Compare con el ejercicio 3). Get 1.7.66 exercise solution
67. Use el ejercicio 64 para encontrar una fórmula para
Get 1.7.67 exercise solution
68. Pruebe que si p y q son divisibles entre k, entonces p + q es divisible entre k. Get 1.7.68 exercise solution
