Soluciones Matemáticas Discretas 6ed Johnsonbaugh -Solucionario: Soluciones Ejercicios Capítulo 1.4 Matemáticas Discretas Johnsonbaugh 6 ed

Sea T(x, y) la función proposicional “x es más alto que y, y x y”. El
dominio de discurso consiste en tres estudiantes: Gerardo, que mide 5
pies 11 pulgadas; Ernesto, que mide 5 pies 6 pulgadas, y Martín que
mide 6 pies. Escriba cada proposición en los ejercicios 1 al 4 en palabras
y diga si ésta es verdadera o falsa.

Get 1.4.1 exercise solution

Get 1.4.2 exercise solution

Get 1.4.3 exercise solution

Get 1.4.4 exercise solution

5. Escriba la negación de cada proposición en los ejercicios del 1 al 4 en palabras y con símbolos.
Sea T(x, y) la función proposicional “x es más alto o de la misma altura que y”. El dominio de discurso consiste en tres estudiantes: Gerardo, que mide 5 pies 11 pulgadas; Ernesto, que mide 5 pies 6 pulgadas, y Martín que mide 6 pies. Get 1.4.5 exercise solution

Escriba cada proposición en los ejercicios 6 al 9 en palabras y diga si ésta es verdadera o falsa.

Get 1.4.6 exercise solution

Get 1.4.7 exercise solution

Get 1.4.8 exercise solution

Get 1.4.9 exercise solution

10. Escriba la negación de cada proposición en los ejercicios 6 al 9 en palabras y con símbolos.
Sea L(x, y) la función proposicional “x ama a y”. El dominio de discurso es el conjunto de todas las personas amantes. Escriba cada proposición en los ejercicios 11 al 14 con símbolos. ¿Cuál piensa que sea verdadera?

11. Alguien ama a todos. Get 1.4.11 exercise solution

12. Todos aman a todos. Get 1.4.12 exercise solution

13. Alguien ama a alguien. Get 1.4.13 exercise solution

14. Todos aman a alguien. Get 1.4.14 exercise solution

15. Escriba la negación de cada proposición en los ejercicios 11 al 14 en palabras y con símbolos. Get 1.4.15 exercise solution

Sea P(x, y) la función proposicional x ≥ y. El dominio de discurso es el conjunto de todos los enteros positivos. Diga si cada proposición en los ejercicios 16 al 19 es verdadera o falsa.

Get 1.4.16 exercise solution

Get 1.4.17 exercise solution

Get 1.4.18 exercise solution

Get 1.4.19 exercise solution

20. Escriba la negación de cada proposición en los ejercicios 16 al 19. Get 1.4.20 exercise solution

Determine el valor de verdad de cada afirmación en los ejercicios 21 al 38. El dominio de discurso es el conjunto de números reales. Justifique sus respuestas.

Get 1.4.21 exercise solution

Get 1.4.22 exercise solution

Get 1.4.23 exercise solution

Get 1.4.24 exercise solution

Get 1.4.25 exercise solution

Get 1.4.26 exercise solution

Get 1.4.27 exercise solution

Get 1.4.28 exercise solution

Get 1.4.29 exercise solution

Get 1.4.30 exercise solution

Get 1.4.31 exercise solution

Get 1.4.32 exercise solution

Get 1.4.33 exercise solution

Get 1.4.34 exercise solution

Get 1.4.35 exercise solution

Get 1.4.36 exercise solution

Get 1.4.37 exercise solution

Get 1.4.38 exercise solution

39. Escriba la negación de cada proposición en los ejercicios 21 al 38. Get 1.4.39 exercise solution

40. Suponga que P es una función proposicional cuyo dominio de discurso consiste en los elementos d1, ..., dn. Escriba el seudocódigo que determina si
∃x∀y P(x, y)
es verdadera o falsa. Get 1.4.40 exercise solution

41. Suponga que P es una función proposicional cuyo dominio de discurso consiste en los elementos d1, ..., dn. Escriba el seudocódigo que determina si
∃x∃y P(x, y)
es verdadera o falsa. Get 1.4.41 exercise solution

42. Explique cómo determina el juego de lógica (ejemplo 1.4.15) si cada proposición en los ejercicios 21 al 38 es verdadera o falsa. Get 1.4.42 exercise solution

43. Use el juego de lógica (ejemplo 1.4.15) para determinar si la proposición ∀x∀y∃z((z > x) ∧ (z < y)) es verdadera o falsa. El dominio de discurso es el conjunto de todos los enteros. Get 1.4.43 exercise solution

44. Use el juego de lógica (ejemplo 1.4.15) para determinar si la proposición ∀x∀y∃z((z < x) ∧ (z < y)) es verdadera o falsa. El dominio de discurso es el conjunto de todos los enteros. Get 1.4.44 exercise solution

45. Use el juego de lógica (ejemplo 1.4.15) para determinar si la proposición
∀x∀y∃z((x < y) → ((z > x) ∧ (z < y))) es verdadera o falsa. El dominio de discurso es el conjunto de todos los enteros. Get 1.4.45 exercise solution

46. Use el juego de lógica (ejemplo 1.4.15) para determinar si la proposición
∀x∀y∃z((x < y) → ((z > x) ∧ (z < y))) es verdadera o falsa. El dominio de discurso es el conjunto de todos los números reales. Get 1.4.46 exercise solution

Suponga que ∀x∀y P(x, y) es verdadera y que el dominio de discurso es no vacío. ¿Cuál de los ejercicios entre el 47 y el 49 debe ser verdadero también? Si la afirmación es verdadera, explique, de otra manera, dé un contraejemplo.

Get 1.4.47 exercise solution

Get 1.4.48 exercise solution

Get 1.4.49 exercise solution

Suponga que ∀x∃y P(x, y) es verdadera y que el dominio de discurso es no vacío. ¿Cuál de los ejercicios entre el 50 y el 52 debe ser verdadero también? Si la afirmación es verdadera, explique de otra manera, dé un contraejemplo.

Get 1.4.50 exercise solution

Get 1.4.51 exercise solution

Get 1.4.52 exercise solution

Suponga que ∃x∀y P(x, y) es verdadera y que el dominio de discurso es no vacío. ¿Cuál de los ejercicios entre el 53 y el 55 debe ser verdadero también? Si la afirmación es verdadera, explique; de otra manera, dé un contraejemplo.

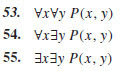
Get 1.4.53 exercise solution

Get 1.4.54 exercise solution

Get 1.4.55 exercise solution

Suponga que ∃x∃y P(x, y) es verdadera y que el dominio de discurso es no vacío. ¿Cuál de los ejercicios entre el 56 y el 58 debe ser verdadero también? Si la afirmación es verdadera, explique; de otra manera, dé un contraejemplo.