




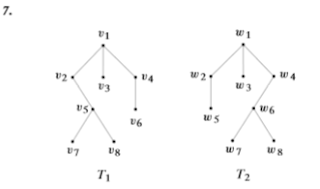
En los ejercicios 7 al 9, determine si cada par de árboles con raíz es isomorfo. Si lo es, especifique un isomorfismo. Si el par no es isomorfo, dé una invariante que un árbol satisfaga y el otro no. Además, determine si los árboles son isomorfos como árboles libres.
8. T1 y T2 como en el ejercicio 3

En los ejercicios 10 al 12, determine si cada par de árboles binarios es isomorfo. Si lo es, especifique un isomorfismo. Si el par no es isomorfo, dé una invariante que un árbol satisfaga y el otro no. Además, determine si los árboles son isomorfos como árboles libres o como árboles con raíz.
10. T1 y T2 como en el ejercicio 9


13. Dibuje todos los árboles libres no isomorfos de 3 vértices.
14. Dibuje todos los árboles libres no isomorfos de 4 vértices.
15. Dibuje todos los árboles libres no isomorfos de 6 vértices.
16. Dibuje todos los árboles con raíz no isomorfos de 3 vértices.
17. Dibuje todos los árboles con raíz no isomorfos de 5 vértices.
18. Dibuje todos los árboles binarios no isomorfos de 2 vértices.
19. Dibuje todos los árboles binarios no isomorfos de 4 vértices.
20. Dibuje todos los árboles binarios completos no isomorfos de 7 vértices. (Un árbol binario completo es un árbol binario en el que cada vértice interno tiene dos hijos).
21. Dibuje todos los árboles binarios completos no isomorfos de 9 vértices.
23. Encuentre todos los árboles de expansión (como árboles libres, no como árboles con raíz) no isomorfos par cada gráfica en los ejercicios 7 al 9, sección 9.3.
24. Utilice inducción para demostrar que cuando dos árboles binarios isomorfos de kvértices se introducen al algoritmo 9.8.13, el número de comparaciones con nulo es igual a 6k+2.
25. Demuestre que cuando los dos árboles binarios que aparecen en la figura 9.8.15 son la entrada del algoritmo 9.8.13, el número de comparaciones con nulo es igual a 6k+4.
26. Escriba un algoritmo para generar un árbol binario aleatorio de n vértices.
27. Un árbol ordenado es un árbol que toma en cuenta el orden de los hijos. Por ejemplo, los árboles ordenados
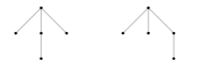
son no isomorfos. Demuestre que el número de árboles ordenados no isomorfos con n aristas es igual a Cn, el n-ésimo número de Catalan. Sugerencia: Considere un recorrido de preorden de árbol ordenado en el que 1 significa abajo y 0 significa arriba.
28. [Proyecto] Informe acerca de las fórmulas para el número de árboles libres no isomorfos y para el número de árboles con raíz no isomorfos de n vértices (vea [Deo]).