




En los ejercicios 6 al 8, determine si la gráfica es plana. Si lo es, dibújela de nuevo sin que se crucen las aristas; de otra manera, encuentre una subgráfica homomorfa a K5 o bien K3,3.



11. Demuestre que cualquier gráfica que tiene 4 vértices o menos es plana.
12. Demuestre que cualquier gráfica que tiene 5 vértices o menos y un vértice de grado 2 es plana.
13. Demuestre que en cualquier gráfica simple, conexa, plana, e ≤ 3v −6.
14. Dé un ejemplo de una gráfica simple, conexa y no plana para la que e ≥ 3v −6.
15. Use el ejercicio 13 para demostrar que K5 no es plana.
16. Demuestre que si una gráfica simple G tiene 11 vértices o más, entonces una de las dos, G o su complemento G , no es plana.
17. Demuestre que si una gráfica plana tiene un ciclo de Euler, tiene un ciclo de Euler sin cruces. Una trayectoria P en una gráfica plana tiene un cruce si un vértice v aparece al menos dos veces en P y P se cruza a sí misma en v; es decir,
P =(..., w1, v, w2, ..., w3, v, w4, ...),
donde los vértices se arreglan de manera que w1, v, w2 cruza a w3, v, w4 en v como en la figura siguiente.

Un coloreado de una gráfica G con los colores C1, C2, . . . , Cn asigna a cada vértice un color Ci de manera que cada vértice tiene un color diferente del de los vértices adyacentes. Por ejemplo, la siguiente gráfica tiene tres colores. El resto de los ejercicios tienen que ver con colorear gráficas.

Un mapa plano es una gráfica plana donde las caras se interpretan como los países, las aristas son las fronteras entre esos países y los vértices representan las intersecciones de las fronteras. El problema de colorear un mapa plano G, de manera que los países con fronteras comunes no tengan el mismo color, se puede reducir al problema de colorear una gráfica construyendo primero la gráfica dual G de G de la siguiente manera. Los vértices de la gráfica dual G consisten en un punto en cada cara de G, incluso en la cara no acotada. Una arista en G conecta dos vértices si las caras correspondientes en G están separadas por una frontera. Colorear el mapa G es equivalente a colorear los vértices de la gráfica dual G .

20. Demuestre que cualquier coloreado del mapa del ejercicio 18, excepto la región no acotada, requiere al menos 3 colores.
21. Coloree el mapa del ejercicio 18, excepto la región no acotada, usando tres colores.
22. Encuentre el dual del siguiente mapa.
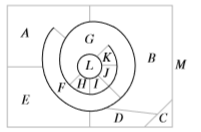
23. Demuestre que cualquier coloreado del mapa del ejercicio 22, excepto la región no acotada, requiere al menos 4 colores.
24. Coloree el mapa del ejercicio 22, excepto la región no acotada, usando 4 colores. Una triangulación de una gráfica G plana simple se obtiene de G conectando el mayor número de vértices posible al tiempo que se mantiene la naturaleza plana al no introducir lazos o aristas paralelas.
25. Encuentre una triangulación de la siguiente gráfica.

27. Demuestre que en una triangulación de una gráfica G plana simple, 3f=2e. Appel y Haken probaron (vea [Appel]) que toda gráfica plana simple se puede colorear con cuatro colores. El problema se planteó a mediados del siglo XIX y durante años nadie tuvo éxito en dar una prueba. Quienes trabajan en el problema de cuatro colores en años recientes han tenido una ventaja sobre sus predecesores: el uso de las computadoras electrónicas rápidas. El siguiente ejercicio muestra cómo comienza la prueba. Suponga que se tiene una gráfica plana simple que requiere más de cuatro colores para colorearla. Entre este tipo de gráficas, existe una con el número mínimo de vértices. Sea G una triangulación de esta gráfica. Entonces G también tiene el número mínimo de vértices y por el ejercicio 26, G requiere más de cuatro colores para colorearla.
28. Si el dual de un mapa tiene un vértice de grado 3, ¿cuál es la apariencia del mapa original?
29. Demuestre que G no tiene un vértice de grado 3.
30. Demuestre que G no tiene un vértice de grado 4.
31. Demuestre que G tiene un vértice de grado 5. La contribución de Appel y Haken fue demostrar que sólo era necesario considerar y analizar un número finito de casos que incluyen el vértice de grado 5, y demostrar que todos se pueden colorear usando 4 colores. La reducción a un número finito de casos se facilitó al usar la computadora para ayudar a encontrar los casos que requieren análisis. De nuevo se usó la computadora para analizar los casos que resultan.
32. Demuestre que cualquier gráfica simple plana se puede colorear usando 5 colores.