1. Dibuje un árbol de juego completo para una versión de nim en la que la posición inicial consiste en una pila de seis fichas y un turno consiste en tomar una, dos o tres. Asigne valores a todos los vértices de manera que el árbol obtenido sea análogo al de la figura 9.9.2. Suponga que el último jugador en tomar una ficha pierde. ¿Ganará siempre el primero o el segundo jugador siguiendo una estrategia óptima? Describa una estrategia óptima para el jugador que gana.
2. Dibuje un árbol de juego completo para nim donde la posición inicial consiste en dos pilas de tres fichas cada una. Omita las posiciones simétricas. Suponga que el último jugador en tomar una ficha pierde. Asigne valores a todos los vértices de modo que el árbol que obtenga sea análogo al de la figura 9.9.2. ¿Ganará siempre el primero o el segundo jugador siguiendo una estrategia óptima? Describa una estrategia óptima para el jugador que gana.
3. Dibuje un árbol de juego completo para nim donde la posición inicial consiste en dos pilas, una con tres fichas y la otra con dos. Suponga que el último jugador en tomar una ficha gana. Asigne valores a todos los vértices de modo que el árbol que obtenga sea análogo al de la figura 9.9.2. ¿Ganará siempre el primero o el segundo jugador siguiendo una estrategia óptima? Describa una estrategia óptima para el jugador que gana.
4. Dibuje un árbol de juego completo para nim donde la posición inicial consiste en dos pilas de tres fichas cada una. Omita las posiciones simétricas. Suponga que el último jugador en tomar una ficha gana. Asigne valores a todos los vértices de modo que el árbol que obtenga sea análogo al de la figura 9.9.2. ¿Ganará siempre el primero o el segundo jugador siguiendo una estrategia óptima? Describa una estrategia óptima para el jugador que gana.
5. Dibuje un árbol de juego completo para la versión de nim descrita en el ejercicio 1. Suponga que el último jugador en tomar una ficha gana. Asigne valores a todos los vértices de modo que el árbol que obtenga sea análogo al de la figura 9.9.2. ¿Ganará siempre el primero o el segundo jugador siguiendo una estrategia óptima? Describa una estrategia óptima para el jugador que gana.
6. Dé un ejemplo de un árbol de juego completo (posiblemente hipotético) en el que un vértice terminal es 1 si el primer jugador gana y 0 si el primer jugador pierde con las siguientes propiedades: hay más ceros que unos en los vértices terminales, pero el primer jugador siempre puede ganar si sigue una estrategia óptima.
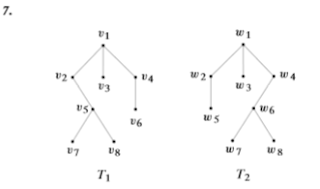
Los ejercicios 7 y 8 se refieren a nim y nim’. Nim es el juego que usa n pilas de fichas como se describe en esta sección, en donde el último jugador que mueve pierde. Nim’es el juego que usa n pilas de fichas como se describe en esta sección excepto que el último jugador que mueve gana. Se fijan n pilas con un número fijo de fichas. Se supone que al menos una pila tiene al menos dos fichas.
7. Demuestre que el primer jugador puede ganar siempre en nim si y sólo si el primer jugador puede ganar siempre en nim’.
8. Dada una estrategia ganadora para un jugador de nim en particular, describa una estrategia ganadora para este jugador de nim’. Evalúe cada vértice en cada árbol de juego. Los valores de los vértices terminales están dados.
Get 9.9.8 exercise solution





14. Evalúe la raíz de cada uno de los árboles de los ejercicios 9 al 13 mediante una búsqueda a profundidad con recorte alfa-beta. Suponga que los hijos se evalúan de izquierda a derecha. Para cada vértice cuyo valor se calcula, escriba el valor en el vértice. Marque la raíz de cada subárbol que se recorta. El valor de cada vértice terminal se escribe abajo del vértice.
En los ejercicios 15 al 18, determine el valor de la posición en el gato usando la función de evaluación del ejemplo 9.9.1.




19. Suponga que el primer jugador se mueve al centro del cuadro del gato. Dibuje un árbol de juego de dos niveles, con la raíz que tiene una X en el centro del cuadro. Omita las posiciones simétricas. Evalúe todos los vértices mediante la función de evaluación del ejemplo 9.9.1. ¿Hacia dónde se moverá O?
20. Un programa de búsqueda de dos niveles basado en la función de evaluación E del ejemplo 9.9.1, ¿jugará un juego perfecto de gato? Si no es así, ¿puede alterar E de manera que un programa de búsqueda de dos niveles juegue un juego perfecto?
21. Escriba un algoritmo que evalúe los vértices de un árbol de juego hasta el nivel n usando una búsqueda a profundidad. Suponga que existe una función de evaluación E.
22. Escriba un algoritmo que evalúe la raíz de un árbol de juego usando una búsqueda a lo largo de nivel ncon recorte alfa-beta. Suponga que existe una función de evaluación E.
El siguiente enfoque con frecuencia conduce a más recortes que el de minimax alfa-beta puro. Primero, se realiza una búsqueda de dos niveles. Se evalúan los hijos de izquierda a derecha. En este punto, todos los hijos de la raíz tendrán valores. Después, se ordenan los hijos de la raíz con los movimientos más promisorios a la izquierda. Ahora, se utiliza una búsqueda a profundidad de n niveles con recorte alfa-beta. Se evalúan los hijos de izquierda a derecha.
Se realiza este procedimiento para n=4 por cada árbol de juego de los ejercicios 23 al 25. Se coloca una marca junto a la raíz de cada subárbol que se recorta. El valor de cada vértice, según lo da la función de evaluación, se coloca abajo del vértice



26. Escriba un algoritmo para realizar el procedimiento descrito en el ejercicio 23.
Mu Torere es un juego de dos personas jugado por los maoríes (vea [Bell]). El tablero es una estrella de ocho picos con un área circular en el centro conocida como putahi.

El primer jugador tiene cuatro fichas negras y el segundo tiene cuatro fichas blancas. La posición inicial se muestra en la estrella. Un jugador que no puede hacer un movimiento pierde. Los jugadores alternan movimientos. Cuando mucho una ficha puede ocupar un pico de la estrella o el putahi. Un movimiento consiste en a) Moverse al pico adyacente b) Moverse del putahi a un pico c) Moverse de un pico al putahi siempre que uno o ambos picos adyacentes contengan piezas del oponente
27. Desarrolle una función de evaluación para Mu Torere.
28. Combine la función de evaluación del ejercicio 27 con una búsqueda de dos niveles del árbol de juego para obtener un algoritmo que permita jugar Mu Torere. Evalúe la habilidad para jugar de este algoritmo.
29. ¿Puede el primer jugador ganar siempre en Mu Torere?
30. ¿Puede el primer jugador empatar siempre en Mu Torere?
31. [Proyecto] Según [Nilsson], el árbol de juego completo para el ajedrez tiene más de 10100 vértices. Haga un informe acerca de cómo se obtuvo esta estimación.
32. [Proyecto] Desarrolle una función de evaluación para Kalah. (Vea las reglas en [Ainslie]).
33. Desarrolle un algoritmo que juegue Kalah basado en la función de evaluación del ejercicio 32. Evalúe la habilidad para jugar de este algoritmo.