1. Sea S un conjunto finito de puntos en el plano. Sea p1 el punto con la coordenada y mínima. Si varios puntos tienen la misma coordenada y mínima, elija el que tiene la menor coordenada x. Pruebe que p1 está en el casco convexo de S.
2. Pruebe el Teorema 13.2.5 para x1 =x0.
3. Pruebe el Teorema 13.2.5 para x1 > x0.
4. Use el algoritmo de Graham para encontrar el casco convexo de los puntos
(10, 1), (7, 7), (3, 13), (6, 10), (16, 4), (10, 5), (7, 13), (13, 8), (4, 4), (2, 2), (1, 8), (10, 13), (7, 1), (4, 8), (12, 3), (16, 10), (14, 5), (10, 9).
5. Utilice el algoritmo de Graham para encontrar el casco convexo de los puntos
(7, 8), (9, 8), (3, 11), (5, 1), (7, 11), (9, 5), (9, 1), (6, 7), (4, 5), (2, 1), (10, 17), (7, 3), (7, 14), (4, 8), (11, 3), (10, 12).
6. Suponga que el algoritmo de Graham se usó para encontrar el casco convexo de un conjunto S de n puntos. Demuestre que si se agrega un punto a S para obtener S′, el casco convexo de S′ se puede encontrar en un tiempo o(n).
Los ejercicios 7 al 10 se refieren a la marcha de Jarvis, otro algoritmo que calcula el casco convexo de un conjunto finito de puntos en el plano. Al igual que el algoritmo de Graham, comienza por encontrar el punto con la coordenada y mínima. Si ésta es igual para varios puntos se elige la que tiene la coordenada x mínima. Después, la marcha de Jarvis encuentra el punto p2 tal que el ángulo de la horizontal al segmento de recta p1, p2 es mínimo. (En caso de empates, se selecciona el punto más alejado de p1). Después de encontrar p1, . . . , pi, la marcha de Jarvis encuentra el punto pi+1 tal que pi−1, pi, pi+1 hacen el menor giro a la izquierda. (En caso de empates, se elige el punto más alejado de pi).
7. Demuestre que la marcha de Jarvis, de hecho, encuentra el casco convexo.
8. Escriba un seudocódigo para la marcha de Jarvis.
9. Encuentre el tiempo en el peor caso para la marcha de Jarvis.
10. ¿Existen conjuntos para los que la marcha de Jarvis sea más rápida que el algoritmo de Graham? Explique su respuesta.
Soluciones Ejercicios Capítulo 13.1 Matemáticas Discretas Johnsonbaugh 6 ed
1. Describa cómo el algoritmo del par más cercano encuentra el par más cercano entre los puntos si la entrada es (8, 4), (3, 11), (12, 10), (5, 4), (1, 2), (17, 10), (8, 7), (8, 9), (11, 3), (1, 5), (11, 7), (5, 9), (1, 9), (7, 6), (3, 7), (14, 7),
2. ¿Qué se puede concluir de la entrada al algoritmo del par más cercano cuando la salida es cero para las distancias entre un par más cercano?
3. Dé un ejemplo de una entrada para la que el algoritmo del par más cercano coloca algunos puntos que están sobre la línea divisoria l en la mitad izquierda y otros en la derecha.
4. Explique por qué, en algunos casos, al dividir un conjunto de puntos con una línea vertical en dos partes casi iguales, es necesario que la línea contenga algunos de los puntos.
5. Escriba un algoritmo del par más cercano que encuentre un par más cercano al igual que la distancia entre el par de puntos.
6. Escriba un algoritmo que encuentre la distancia entre un par más cercano de puntos en una línea (recta).
7. Dé un ejemplo de la entrada para la cual comparar cada punto en la franja con los siguientes dos puntos produce una salida incorrecta.
8. Dé un ejemplo para demostrar que es posible colocar seis puntos en el rectángulo de la figura 13.1.2 cuando se incluye la base y se excluyen los otros lados.
9. Cuando se calculan las distancias entre un punto p en la franja y los puntos que le siguen, ¿se puede dejar de calcular las distancias desde p si se encuentra un punto q tal que la distancia entre p y q excede a δ? Explique su respuesta.
10. Demuestre que hay cuando mucho seis puntos en el rectángulo de la figura 13.1.2 cuando se incluye la base y los otros lados se excluyen.
11. Escriba un algoritmo (n lg n) que encuentre la distancia δ entre un par más cercano y que, si δ>0, también encuentre todos los pares que están a una distancia δ.
12. Escriba un algoritmo (n lg n) que encuentre la distancia δ entre un par más cercano y todos los pares que están a menos de 2δ.
13. Escriba un algoritmo (n lg n) que encuentre la distancia δ entre un par más cercano y todos los pares a menos de 2δ, donde cada par que está a menos de 2δ se lista exactamente una vez.
14. Explique por qué el siguiente algoritmo no encuentra la distancia δ entre un par más cercano y todos los pares a menos de 2δ.
ejercicio14(p, n) {
δ =par_más_cercano(p, n)
for i=1 to n−1
for j=i+1 to mín{n, i+31}
if (dist(pi, pj) < 2*δ)
println(i+“ ” +j)
}
15. Escriba un algoritmo que combine encontrar los puntos en la franja y buscar en la franja. De esta manera, el tamaño de la franja cambia en forma dinámica de modo que, en general, esta versión verifica menos puntos en la franja que el algoritmo 13.1.2.
16. Suponga que la distancia entre un par más cercano en un conjunto de n puntos en el plano es δ>0. Demuestre que el número de pares que están exactamente a una distancia δ es O(n).
2. ¿Qué se puede concluir de la entrada al algoritmo del par más cercano cuando la salida es cero para las distancias entre un par más cercano?
3. Dé un ejemplo de una entrada para la que el algoritmo del par más cercano coloca algunos puntos que están sobre la línea divisoria l en la mitad izquierda y otros en la derecha.
4. Explique por qué, en algunos casos, al dividir un conjunto de puntos con una línea vertical en dos partes casi iguales, es necesario que la línea contenga algunos de los puntos.
5. Escriba un algoritmo del par más cercano que encuentre un par más cercano al igual que la distancia entre el par de puntos.
6. Escriba un algoritmo que encuentre la distancia entre un par más cercano de puntos en una línea (recta).
7. Dé un ejemplo de la entrada para la cual comparar cada punto en la franja con los siguientes dos puntos produce una salida incorrecta.
8. Dé un ejemplo para demostrar que es posible colocar seis puntos en el rectángulo de la figura 13.1.2 cuando se incluye la base y se excluyen los otros lados.
9. Cuando se calculan las distancias entre un punto p en la franja y los puntos que le siguen, ¿se puede dejar de calcular las distancias desde p si se encuentra un punto q tal que la distancia entre p y q excede a δ? Explique su respuesta.
10. Demuestre que hay cuando mucho seis puntos en el rectángulo de la figura 13.1.2 cuando se incluye la base y los otros lados se excluyen.
11. Escriba un algoritmo (n lg n) que encuentre la distancia δ entre un par más cercano y que, si δ>0, también encuentre todos los pares que están a una distancia δ.
12. Escriba un algoritmo (n lg n) que encuentre la distancia δ entre un par más cercano y todos los pares que están a menos de 2δ.
13. Escriba un algoritmo (n lg n) que encuentre la distancia δ entre un par más cercano y todos los pares a menos de 2δ, donde cada par que está a menos de 2δ se lista exactamente una vez.
14. Explique por qué el siguiente algoritmo no encuentra la distancia δ entre un par más cercano y todos los pares a menos de 2δ.
ejercicio14(p, n) {
δ =par_más_cercano(p, n)
for i=1 to n−1
for j=i+1 to mín{n, i+31}
if (dist(pi, pj) < 2*δ)
println(i+“ ” +j)
}
15. Escriba un algoritmo que combine encontrar los puntos en la franja y buscar en la franja. De esta manera, el tamaño de la franja cambia en forma dinámica de modo que, en general, esta versión verifica menos puntos en la franja que el algoritmo 13.1.2.
16. Suponga que la distancia entre un par más cercano en un conjunto de n puntos en el plano es δ>0. Demuestre que el número de pares que están exactamente a una distancia δ es O(n).
Soluciones Ejercicios Capítulo 12.5 Matemáticas Discretas Johnsonbaugh 6 ed
1. Encuentre el autómata de estado finito equivalente al autómata de estado finito no determinístico en los ejercicios 1 al 10, de la sección 12.4. En los ejercicios 2 al 6, encuentre el autómata de estado finito que acepte las cadenas generadas por gramáticas regulares.
2. La gramática del ejercicio 1, sección 12.3.
3. La gramática del ejercicio 5, sección 12.3.
4. <S> ::= a< A>|a<B>
< A> ::= a<B>|b<S>|b
<B> ::= b<S>|b
con símbolo de inicio < S >
5. <S> ::= a<S>|a< A>|b<C>|a
< A> ::= b< A>|a<C>
<B> ::= a<S>|a
<C> ::= a<B>|a<C>
con símbolo de inicio < S >
6. <S> ::= a< A>|a<B>
< A> ::= b<S>|b
<B> ::= a<B>|a<C>
<C> ::= a<S>|b< A>|a<C>|a
con símbolo de inicio < S >
7. Encuentre autómatas de estado finito que acepten las cadenas de los ejercicios 21 al 29, de la sección 12.4.
8. Elimine los estados que no se alcanzan del autómata de estado finito de la figura 12.5.3 para encontrar un autómata de estado finito equivalente, más sencillo.
9. Demuestre que el autómata de estado finito no determinístico de la figura 12.5.5 acepta una cadena α sobre {a, b} si y sólo si α comienza con bb.
10. Caracterice las cadenas aceptadas por los autómatas de estado finito no determinísticos de las figuras 12.5.7 y 12.5.9.
En los ejercicios 11 al 21, encuentre un autómata de estado finito no determinístico que acepte el conjunto dado de cadenas. Si S1 y S2 son conjuntos de cadenas, sea
S+ 1 ={ u1u2···un |ui ∈ S1, n ∈{1, 2, ...}};
S1S2 ={ uv |u ∈ S1, v ∈ S2}.
11. Ac(A)R, donde A es el autómata del ejercicio 4, sección 12.2
12. Ac(A)R, donde A es el autómata del ejercicio 5, sección 12.2
13. Ac(A)R, donde A es el autómata del ejercicio 6, sección 12.2
14. Ac(A)+, donde A es el autómata del ejercicio 4, sección 12.2
15. Ac(A)+, donde A es el autómata del ejercicio 5, sección 12.2
16. Ac(A)+, donde A es el autómata del ejercicio 6, sección 12.2
Get 12.5.16 exercise solution
17. Ac(A)+, donde A es el autómata de la figura 12.5.7
18. Ac(A1)Ac(A2), donde A1 es el autómata del ejercicio 4, sección 12.2, y A2 es el autómata del ejercicio 5, sección 12.2
19. Ac(A1)Ac(A2), donde A1 es el autómata del ejercicios 5, sección 12.2, y A2 es el autómata del ejercicio 6, sección 12.2
20. Ac(A1)Ac(A1), donde A1 es el autómata del ejercicios 6, sección 12.2
21. Ac(A1)Ac(A2), donde A1 es el autómata de la figura 12.5.7 y A2 es el autómata del ejercicio 5, sección 12.2
22. Encuentre una gramática regular que genere el lenguaje LR, donde L es el lenguaje generado por la gramática del ejercicio 5, sección 12.3.
23. Encuentre una gramática regular que genere el lenguaje L+, donde L es el lenguaje generado por la gramática del ejercicio 5, sección 12.3.
24. Sea L1 (respectivamente, L2) el lenguaje generado por la gramática del ejercicio 5, sección 12.3 (respectivamente, ejemplo 12.5.5). Encuentre una gramática regular que genere el lenguaje L1L2.
25. Demuestre que el conjunto
L ={ x1···xn | x1···xn = xn···x1}
de cadenas sobre {a, b} no es un lenguaje regular.
26. Demuestre que si L1 y L2 son lenguajes regulares sobre Iy S es el conjunto de todas las cadenas sobre I, entonces cada uno de S – L1, L1 ∪L2, L1 ∩L2, L1+ y L1L2 es un lenguaje regular.
27. Demuestre, con un ejemplo, que existen lenguajes libres de contexto L1 y L2 tales que L1 ∩L2 no es libre de contexto.
28. Pruebe o desapruebe: si L es un lenguaje regular, también lo es
{un |u ∈ L, n ∈{1, 2, ...}}.
2. La gramática del ejercicio 1, sección 12.3.
3. La gramática del ejercicio 5, sección 12.3.
< A> ::= a<B>|b<S>|b
<B> ::= b<S>|b
con símbolo de inicio < S >
5. <S> ::= a<S>|a< A>|b<C>|a
< A> ::= b< A>|a<C>
<B> ::= a<S>|a
<C> ::= a<B>|a<C>
con símbolo de inicio < S >
6. <S> ::= a< A>|a<B>
< A> ::= b<S>|b
<B> ::= a<B>|a<C>
<C> ::= a<S>|b< A>|a<C>|a
con símbolo de inicio < S >
7. Encuentre autómatas de estado finito que acepten las cadenas de los ejercicios 21 al 29, de la sección 12.4.
8. Elimine los estados que no se alcanzan del autómata de estado finito de la figura 12.5.3 para encontrar un autómata de estado finito equivalente, más sencillo.
9. Demuestre que el autómata de estado finito no determinístico de la figura 12.5.5 acepta una cadena α sobre {a, b} si y sólo si α comienza con bb.
10. Caracterice las cadenas aceptadas por los autómatas de estado finito no determinísticos de las figuras 12.5.7 y 12.5.9.
En los ejercicios 11 al 21, encuentre un autómata de estado finito no determinístico que acepte el conjunto dado de cadenas. Si S1 y S2 son conjuntos de cadenas, sea
S+ 1 ={ u1u2···un |ui ∈ S1, n ∈{1, 2, ...}};
S1S2 ={ uv |u ∈ S1, v ∈ S2}.
11. Ac(A)R, donde A es el autómata del ejercicio 4, sección 12.2
12. Ac(A)R, donde A es el autómata del ejercicio 5, sección 12.2
13. Ac(A)R, donde A es el autómata del ejercicio 6, sección 12.2
14. Ac(A)+, donde A es el autómata del ejercicio 4, sección 12.2
15. Ac(A)+, donde A es el autómata del ejercicio 5, sección 12.2
16. Ac(A)+, donde A es el autómata del ejercicio 6, sección 12.2
Get 12.5.16 exercise solution
17. Ac(A)+, donde A es el autómata de la figura 12.5.7
18. Ac(A1)Ac(A2), donde A1 es el autómata del ejercicio 4, sección 12.2, y A2 es el autómata del ejercicio 5, sección 12.2
19. Ac(A1)Ac(A2), donde A1 es el autómata del ejercicios 5, sección 12.2, y A2 es el autómata del ejercicio 6, sección 12.2
20. Ac(A1)Ac(A1), donde A1 es el autómata del ejercicios 6, sección 12.2
21. Ac(A1)Ac(A2), donde A1 es el autómata de la figura 12.5.7 y A2 es el autómata del ejercicio 5, sección 12.2
22. Encuentre una gramática regular que genere el lenguaje LR, donde L es el lenguaje generado por la gramática del ejercicio 5, sección 12.3.
23. Encuentre una gramática regular que genere el lenguaje L+, donde L es el lenguaje generado por la gramática del ejercicio 5, sección 12.3.
24. Sea L1 (respectivamente, L2) el lenguaje generado por la gramática del ejercicio 5, sección 12.3 (respectivamente, ejemplo 12.5.5). Encuentre una gramática regular que genere el lenguaje L1L2.
25. Demuestre que el conjunto
L ={ x1···xn | x1···xn = xn···x1}
de cadenas sobre {a, b} no es un lenguaje regular.
26. Demuestre que si L1 y L2 son lenguajes regulares sobre Iy S es el conjunto de todas las cadenas sobre I, entonces cada uno de S – L1, L1 ∪L2, L1 ∩L2, L1+ y L1L2 es un lenguaje regular.
27. Demuestre, con un ejemplo, que existen lenguajes libres de contexto L1 y L2 tales que L1 ∩L2 no es libre de contexto.
28. Pruebe o desapruebe: si L es un lenguaje regular, también lo es
{un |u ∈ L, n ∈{1, 2, ...}}.
Soluciones Ejercicios Capítulo 12.4 Matemáticas Discretas Johnsonbaugh 6 ed
En los ejercicios 1 al 5, dibuje el diagrama de transición del autómata de estado finito no determinístico (I, S, f, A, σ0).





Para cada autómata de estado finito no determinístico en los ejercicios 6 al 10, encuentre los conjuntos I, S, y A, el estado inicial y la tabla que define la función del siguiente estado.

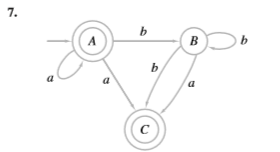



11. Escriba las gramáticas regulares dadas por el autómata de estado finito de los ejercicios 4 al 9, sección 12.2.
12. Represente las gramáticas de los ejercicios 1 y 5, sección 12.3 y el ejemplo 12.3.14 por un autómata de estado finito no determinístico.
13. ¿El autómata de estado finito no determinístico de la figura 12.4.2 acepta la cadena bbabbb? Pruebe su respuesta.
14. ¿El autómata de estado finito no determinístico de la figura 12.4.2 acepta la cadena bbabab? Pruebe su respuesta.
15. Demuestre que una cadena α sobre {a, b} es aceptada por el autómata de estado finito no determinístico de la figura 12.4.2 si y sólo si α contiene exactamente una a y termina con b.
16. ¿La cadena aaabba es aceptada por el autómata de estado finito no determinístico de la figura 12.4.3? Pruebe su respuesta.
17. ¿La cadena aaaab es aceptada por el autómata de estado finito no determinístico de la figura 12.4.3? Pruebe su respuesta.
18. Caracterice las cadenas aceptadas por el autómata de estado finito no determinístico de la figura 12.4.3.
19. Muestre que las cadenas aceptadas por el autómata de estado finito no determinístico del ejercicio 8 son precisamente las cadenas sobre {a, b} que terminan con bab.
20. Caracterice las cadenas aceptadas por el autómata de estado finito no determinístico de los ejercicios 1 al 7, 9 y 10. Diseñe un autómata de estado finito no determinístico que acepte las cadenas sobre {a, b} que tienen las propiedades especificadas en los ejercicios 21 al 29.
21. Comienzan con abb o con ba
22. Terminan con abb o con ba
23. Contienen abb o ba
24. Contienen bab y bb
25. Cada b está precedida y seguida por una a
26. Comienzan con abb y terminan con ab
27. Comienzan con ab pero no terminan con ab
28. No contienen ba ni bbb
29. No contienen abba ni bbb
30. Escriba las gramáticas regulares que generan las cadenas de los ejercicios 21 al 29.





Para cada autómata de estado finito no determinístico en los ejercicios 6 al 10, encuentre los conjuntos I, S, y A, el estado inicial y la tabla que define la función del siguiente estado.





11. Escriba las gramáticas regulares dadas por el autómata de estado finito de los ejercicios 4 al 9, sección 12.2.
12. Represente las gramáticas de los ejercicios 1 y 5, sección 12.3 y el ejemplo 12.3.14 por un autómata de estado finito no determinístico.
13. ¿El autómata de estado finito no determinístico de la figura 12.4.2 acepta la cadena bbabbb? Pruebe su respuesta.
14. ¿El autómata de estado finito no determinístico de la figura 12.4.2 acepta la cadena bbabab? Pruebe su respuesta.
15. Demuestre que una cadena α sobre {a, b} es aceptada por el autómata de estado finito no determinístico de la figura 12.4.2 si y sólo si α contiene exactamente una a y termina con b.
16. ¿La cadena aaabba es aceptada por el autómata de estado finito no determinístico de la figura 12.4.3? Pruebe su respuesta.
17. ¿La cadena aaaab es aceptada por el autómata de estado finito no determinístico de la figura 12.4.3? Pruebe su respuesta.
18. Caracterice las cadenas aceptadas por el autómata de estado finito no determinístico de la figura 12.4.3.
19. Muestre que las cadenas aceptadas por el autómata de estado finito no determinístico del ejercicio 8 son precisamente las cadenas sobre {a, b} que terminan con bab.
20. Caracterice las cadenas aceptadas por el autómata de estado finito no determinístico de los ejercicios 1 al 7, 9 y 10. Diseñe un autómata de estado finito no determinístico que acepte las cadenas sobre {a, b} que tienen las propiedades especificadas en los ejercicios 21 al 29.
21. Comienzan con abb o con ba
22. Terminan con abb o con ba
23. Contienen abb o ba
24. Contienen bab y bb
25. Cada b está precedida y seguida por una a
26. Comienzan con abb y terminan con ab
27. Comienzan con ab pero no terminan con ab
28. No contienen ba ni bbb
29. No contienen abba ni bbb
30. Escriba las gramáticas regulares que generan las cadenas de los ejercicios 21 al 29.
Soluciones Ejercicios Capítulo 12.3 Matemáticas Discretas Johnsonbaugh 6 ed
En los ejercicios 1 al 6, determine si la gramática dada es sensible al contexto, libre de contexto, regular o ninguna de ellas. Dé todas las caracterizaciones pertinentes.






En los ejercicios 7 al 11, demuestre que la cadena α está en L(G) para la gramática G dando una derivación de α.
7. bbabbab, ejercicio 1
8. abab, ejercicio 2
9. aabbaab, ejercicio 3
10. abbbaabab, ejercicio 4
11. abaabbabba, ejercicio 5
12. Escriba las gramáticas de los ejemplos 12.3.4 y 12.3.9 y los ejercicios 1 al 4 y 6 en la BNF.
13. Sea G la gramática del ejercicio 1. Demuestre que α ∈ L(G) si y sólo si α no es nula y contiene un número par de símbolos a.
14. Sea G la gramática del ejercicio 5. Caracterice L(G). En los ejercicios 15 al 24, escriba una gramática que genere las cadenas que tienen la propiedad señalada.
15. Cadenas sobre {a, b} que inician con a
16. Cadenas sobre {a, b} que terminan con ba
17. Cadenas sobre {a, b} que contienen ba
18. Cadenas sobre {a, b} que no terminan con ba
19. Enteros sin ceros a la izquierda
20. Números de punto flotante (números como .294, 89., 67.284)
21. Números exponenciales (números que incluyen punto flotante y números como 6.9E3, 8E12, 9.6E–4, 9E–10)
22. Expresiones booleanas en X1, . . . , Xn
23. Todas las cadenas sobre {a, b}
24. Cadenas x1, . . . , xn sobre {a, b} con x1 · · ·xn =xn · · ·x1
Cada gramática en los ejercicios 25 al 31 se propone como generadora del conjunto L de cadenas sobre {a, b} que contienen el mismo número de símbolos a y b. Si la gramática genera L, demuéstrelo. Si la gramática no genera L, dé un contraejemplo y pruebe que su contraejemplo es correcto. En cada gramática, S es el símbolo de inicio.





Considere a G=(N, T, P, S) como una gramática de Lindenmayer libre de contexto. Interprete el símbolo d como un comando para dibujar una línea recta de longitud fija en la dirección actual; interprete + como un comando para girar 90° a la derecha, e interprete – como un comando para girar 90° a la izquierda. Genere las dos cadenas más pequeñas en L(G) y dibuje las curvas correspondientes. Estas curvas se conocen como islas cuadráticas de Koch.
36. La siguiente figura:

Considere a G=(N, T, P, S) como una gramática de Lindenmayer libre de contexto. Interprete el símbolo d como un comando para dibujar una línea recta de longitud fija en la dirección actual; interprete + como un comando para girar 90° a la derecha, e interprete – como un comando para girar 90° a la izquierda. Genere las dos cadenas más pequeñas en L(G) y dibuje las curvas correspondientes. Estas curvas se conocen como islas cuadráticas de Koch.






En los ejercicios 7 al 11, demuestre que la cadena α está en L(G) para la gramática G dando una derivación de α.
7. bbabbab, ejercicio 1
8. abab, ejercicio 2
9. aabbaab, ejercicio 3
10. abbbaabab, ejercicio 4
11. abaabbabba, ejercicio 5
12. Escriba las gramáticas de los ejemplos 12.3.4 y 12.3.9 y los ejercicios 1 al 4 y 6 en la BNF.
13. Sea G la gramática del ejercicio 1. Demuestre que α ∈ L(G) si y sólo si α no es nula y contiene un número par de símbolos a.
14. Sea G la gramática del ejercicio 5. Caracterice L(G). En los ejercicios 15 al 24, escriba una gramática que genere las cadenas que tienen la propiedad señalada.
15. Cadenas sobre {a, b} que inician con a
16. Cadenas sobre {a, b} que terminan con ba
17. Cadenas sobre {a, b} que contienen ba
18. Cadenas sobre {a, b} que no terminan con ba
19. Enteros sin ceros a la izquierda
20. Números de punto flotante (números como .294, 89., 67.284)
21. Números exponenciales (números que incluyen punto flotante y números como 6.9E3, 8E12, 9.6E–4, 9E–10)
22. Expresiones booleanas en X1, . . . , Xn
23. Todas las cadenas sobre {a, b}
24. Cadenas x1, . . . , xn sobre {a, b} con x1 · · ·xn =xn · · ·x1





Considere a G=(N, T, P, S) como una gramática de Lindenmayer libre de contexto. Interprete el símbolo d como un comando para dibujar una línea recta de longitud fija en la dirección actual; interprete + como un comando para girar 90° a la derecha, e interprete – como un comando para girar 90° a la izquierda. Genere las dos cadenas más pequeñas en L(G) y dibuje las curvas correspondientes. Estas curvas se conocen como islas cuadráticas de Koch.
36. La siguiente figura:

Considere a G=(N, T, P, S) como una gramática de Lindenmayer libre de contexto. Interprete el símbolo d como un comando para dibujar una línea recta de longitud fija en la dirección actual; interprete + como un comando para girar 90° a la derecha, e interprete – como un comando para girar 90° a la izquierda. Genere las dos cadenas más pequeñas en L(G) y dibuje las curvas correspondientes. Estas curvas se conocen como islas cuadráticas de Koch.
Soluciones Ejercicios Capítulo 12.2 Matemáticas Discretas Johnsonbaugh 6 ed
En los ejercicios 1 al 3, demuestre que cada máquina de estado finito es un autómata de estado finito y dibuje de nuevo el diagrama como corresponde.



En los ejercicios 4 al 6, dibuje de nuevo el diagrama del autómata de estado finito como el diagrama de transición de una máquina de estado finito.



En los ejercicios 7 al 9, dibuje el diagrama de transición del autómata de estado finito (I, S, f, A, σ0).



10. Para cada autómata de estado finito en los ejercicios 1 al 6, encuentre los conjuntos I, Sy A, el estado inicial, y la tabla que define la función del siguiente estado.
11. ¿Cuáles de las máquinas de estado finito de los ejercicios 1 al 10, de la sección 12.1, son autómatas de estado finito?
12. ¿Cómo debe verse la tabla de una máquina de estado finito M para que M sea un autómata de estado finito?
En los ejercicios 13 al 17, determine si la cadena que se indica es aceptada por el autómata de estado finito dado.
13. abbaa; figura 12.2.2
14. abbaa; figura 12.2.3
15. aabaabb; figura 12.2.5
16. aaabbbaab; ejercicio 5
17. aaababbab; ejercicio 6
18. Demuestre que el autómata de estado finito de la figura 12.2.2 acepta una cadena α en {a, b} si y sólo si α termina con a.
19. Demuestre que el autómata de estado finito de la figura 12.2.5 acepta una cadena α en {a, b} si y sólo si α termina con bb.
20. Caracterice las cadenas aceptadas por el autómata de estado finito de los ejercicios 1 al 9. En los ejercicios 21 al 31, dibuje el diagrama de transición de un autómata de estado finito que acepte el conjunto dado de cadenas en {a, b}.
21. Número par de símbolos a
22. Exactamente una b
23. Al menos una b
24. Exactamente dos símbolos a
25. Al menos dos símbolos a
26. Contiene m símbolos a, donde m es múltiplo de 3
27. Comienza con baa
28. Contiene abba
29. Toda b va seguida por a
30. Termina con aba
31. Comienza con ab y termina con baa
32. Escriba algoritmos similares al algoritmo 12.2.10, que decidan si los autómatas de estado finito de los ejercicios 1 al 9 aceptan o no una cadena dada.
33. Dé un argumento formal para mostrar que los autómatas de estado finito de las figuras 12.2.6 y 12.2.8 son equivalentes.
34. Sea L un conjunto de cadenas en {a, b}. Demuestre que existe un autómata de estado finito que acepta a L.
35. Sea L el conjunto de cadenas aceptadas por el autómata de estado finito del ejercicio 6. Sea S el conjunto de todas las cadenas en {a, b}. Diseñe un autómata de estado finito que acepte S – L.
36. Sea Li el conjunto de cadenas aceptadas por el autómata de estado finito Ai = (I, Si, fi, Ai, σi), i=1, 2. Sea A= (I, S1 ×S2, f, A, σ), donde f((S1, S2), x) = ( f1(S1, x), f2(S2, x))
A={ (A1, A2) | A1 ∈A1 and A2 ∈A2}
σ = (σ1, σ2).
Demuestre que Ac(A) = L1 ∩L2
37. Sea Li el conjunto de cadenas aceptadas por el autómata de estado finito Ai =(I, Si, fi, Ai, σi), i=1, 2. Sea A= (I, S1 ×S2, f, A, σ),
donde
f((S1, S2), x) = ( f1(S1, x), f2(S2, x))
A={ (A1, A2) | A1 ∈A1 or A2 ∈A2}
σ = (σ1, σ2).
Demuestre que Ac(A) = L1 ∪L2
En los ejercicios 38 al 42, sea Dibuje el diagrama de transición del autómata de estado finito que acepta L1∩L2 y L1 ∪L2.
38. A1 dado en el ejercicio 4; A2 dado en el ejercicio 5
39. A1 dado en el ejercicio 4; A2 dado en el ejercicio 6
40. A1 dado en el ejercicio 5; A2 dado en el ejercicio 6
41. A1 dado en el ejercicio 6; A2 dado en el ejercicio 6
42. A1 dado por la figura 12.5.7, sección 12.5; A2 dado en el ejercicio 6



En los ejercicios 4 al 6, dibuje de nuevo el diagrama del autómata de estado finito como el diagrama de transición de una máquina de estado finito.



En los ejercicios 7 al 9, dibuje el diagrama de transición del autómata de estado finito (I, S, f, A, σ0).



10. Para cada autómata de estado finito en los ejercicios 1 al 6, encuentre los conjuntos I, Sy A, el estado inicial, y la tabla que define la función del siguiente estado.
11. ¿Cuáles de las máquinas de estado finito de los ejercicios 1 al 10, de la sección 12.1, son autómatas de estado finito?
12. ¿Cómo debe verse la tabla de una máquina de estado finito M para que M sea un autómata de estado finito?
En los ejercicios 13 al 17, determine si la cadena que se indica es aceptada por el autómata de estado finito dado.
13. abbaa; figura 12.2.2
14. abbaa; figura 12.2.3
15. aabaabb; figura 12.2.5
16. aaabbbaab; ejercicio 5
17. aaababbab; ejercicio 6
18. Demuestre que el autómata de estado finito de la figura 12.2.2 acepta una cadena α en {a, b} si y sólo si α termina con a.
19. Demuestre que el autómata de estado finito de la figura 12.2.5 acepta una cadena α en {a, b} si y sólo si α termina con bb.
20. Caracterice las cadenas aceptadas por el autómata de estado finito de los ejercicios 1 al 9. En los ejercicios 21 al 31, dibuje el diagrama de transición de un autómata de estado finito que acepte el conjunto dado de cadenas en {a, b}.
21. Número par de símbolos a
22. Exactamente una b
23. Al menos una b
24. Exactamente dos símbolos a
25. Al menos dos símbolos a
26. Contiene m símbolos a, donde m es múltiplo de 3
27. Comienza con baa
28. Contiene abba
29. Toda b va seguida por a
30. Termina con aba
31. Comienza con ab y termina con baa
32. Escriba algoritmos similares al algoritmo 12.2.10, que decidan si los autómatas de estado finito de los ejercicios 1 al 9 aceptan o no una cadena dada.
33. Dé un argumento formal para mostrar que los autómatas de estado finito de las figuras 12.2.6 y 12.2.8 son equivalentes.
34. Sea L un conjunto de cadenas en {a, b}. Demuestre que existe un autómata de estado finito que acepta a L.
35. Sea L el conjunto de cadenas aceptadas por el autómata de estado finito del ejercicio 6. Sea S el conjunto de todas las cadenas en {a, b}. Diseñe un autómata de estado finito que acepte S – L.
36. Sea Li el conjunto de cadenas aceptadas por el autómata de estado finito Ai = (I, Si, fi, Ai, σi), i=1, 2. Sea A= (I, S1 ×S2, f, A, σ), donde f((S1, S2), x) = ( f1(S1, x), f2(S2, x))
A={ (A1, A2) | A1 ∈A1 and A2 ∈A2}
σ = (σ1, σ2).
Demuestre que Ac(A) = L1 ∩L2
37. Sea Li el conjunto de cadenas aceptadas por el autómata de estado finito Ai =(I, Si, fi, Ai, σi), i=1, 2. Sea A= (I, S1 ×S2, f, A, σ),
donde
f((S1, S2), x) = ( f1(S1, x), f2(S2, x))
A={ (A1, A2) | A1 ∈A1 or A2 ∈A2}
σ = (σ1, σ2).
Demuestre que Ac(A) = L1 ∪L2
En los ejercicios 38 al 42, sea Dibuje el diagrama de transición del autómata de estado finito que acepta L1∩L2 y L1 ∪L2.
38. A1 dado en el ejercicio 4; A2 dado en el ejercicio 5
39. A1 dado en el ejercicio 4; A2 dado en el ejercicio 6
40. A1 dado en el ejercicio 5; A2 dado en el ejercicio 6
41. A1 dado en el ejercicio 6; A2 dado en el ejercicio 6
42. A1 dado por la figura 12.5.7, sección 12.5; A2 dado en el ejercicio 6
Soluciones Ejercicios Capítulo 12.1 Matemáticas Discretas Johnsonbaugh 6 ed
En los ejercicios 1 al 5, dibuje el diagrama de transición de la máquina de estado finito (I, O, S, f, g, σ0).





En los ejercicios 6 al 10, encuentre los conjuntos I, O y S, el estado inicial y la tabla que define el siguiente estado y las funciones de salida para cada máquina de estado finito.





En los ejercicios 11 al 20, encuentre la cadena de salida para la cadena de entrada que se indica y la máquina de estado finito.
11. abba; ejercicio 1
12. abba; ejercicio 2
13. aabbaba; ejercicio 3
14. aabbcc; ejercicio 4
15. aabaab; ejercicio 5
16. aaa; ejercicio 6
17. aabbabaab; ejercicio 7
18. baaba; ejercicio 8
19. bbababbabaaa; ejercicio 9
20. cacbccbaabac; ejercicio 10
En los ejercicios 21 al 26, diseñe una máquina de estado finito que tenga las propiedades indicadas. La entrada siempre es una cadena de bits.
21. Produce 1 si entra un número par de unos; de otra manera produce 0.
22. Produce 1 si entran k unos, donde k es un múltiplo de 3; de otra manera produce 0.
23. Produce 1 si entran dos unos o más; de otra manera produce 0.
24. Produce 1 cuando ve 101; de otra manera produce 0.
25. Produce 1 cuando ve 101 y en adelante; de otra manera produce 0.
26. Produce 1 cuando ve primero 0 y hasta que ve otro 0; en adelante, produce 0; en el resto de los casos produce 0.
27. Sea α =x1 · · ·xn una cadena de bits. Sea β =y1 · · ·yn, donde

para i=1, . . . , n. Sea . Demuestre que si γ alimenta a la máquina de estado finito de la figura 12.1.4, la salida es el complemento de 2 de α (considere el algoritmo 11.5.16 una descripción del complemento de 2).
28. Demuestre que no existe una máquina de estado finito que reciba una cadena de bits y produzca 1 siempre que el número de unos sea igual al número de ceros en la entrada, y produzca 0 de otra manera.
29. Demuestre que no hay una máquina de estado finito que realice la multiplicación en serie. En particular, demuestre que no hay una máquina de estado finito que alimenta números binarios

Ejemplo: Si existe tal máquina, para multiplicar 101 ×1001 se alimentaría 11,00,10,01,00,00,00,00. El primer par 11 es el par de los bits en la extrema derecha (101, 1001); el segundo par 00 es el siguiente par de bits (101, 1001); y así sucesivamente. Se amortigua la cadena de entrada con cuatro pares 00 —la longitud del número más grande 1001 que debe multiplicarse—. Como 101 ×1001 =101101, se asevera que se obtiene la salida mostrada en la tabla adyacente.






En los ejercicios 6 al 10, encuentre los conjuntos I, O y S, el estado inicial y la tabla que define el siguiente estado y las funciones de salida para cada máquina de estado finito.





En los ejercicios 11 al 20, encuentre la cadena de salida para la cadena de entrada que se indica y la máquina de estado finito.
11. abba; ejercicio 1
12. abba; ejercicio 2
13. aabbaba; ejercicio 3
14. aabbcc; ejercicio 4
15. aabaab; ejercicio 5
16. aaa; ejercicio 6
17. aabbabaab; ejercicio 7
18. baaba; ejercicio 8
19. bbababbabaaa; ejercicio 9
20. cacbccbaabac; ejercicio 10
En los ejercicios 21 al 26, diseñe una máquina de estado finito que tenga las propiedades indicadas. La entrada siempre es una cadena de bits.
21. Produce 1 si entra un número par de unos; de otra manera produce 0.
22. Produce 1 si entran k unos, donde k es un múltiplo de 3; de otra manera produce 0.
23. Produce 1 si entran dos unos o más; de otra manera produce 0.
24. Produce 1 cuando ve 101; de otra manera produce 0.
25. Produce 1 cuando ve 101 y en adelante; de otra manera produce 0.
26. Produce 1 cuando ve primero 0 y hasta que ve otro 0; en adelante, produce 0; en el resto de los casos produce 0.
27. Sea α =x1 · · ·xn una cadena de bits. Sea β =y1 · · ·yn, donde

para i=1, . . . , n. Sea . Demuestre que si γ alimenta a la máquina de estado finito de la figura 12.1.4, la salida es el complemento de 2 de α (considere el algoritmo 11.5.16 una descripción del complemento de 2).
28. Demuestre que no existe una máquina de estado finito que reciba una cadena de bits y produzca 1 siempre que el número de unos sea igual al número de ceros en la entrada, y produzca 0 de otra manera.
29. Demuestre que no hay una máquina de estado finito que realice la multiplicación en serie. En particular, demuestre que no hay una máquina de estado finito que alimenta números binarios

Ejemplo: Si existe tal máquina, para multiplicar 101 ×1001 se alimentaría 11,00,10,01,00,00,00,00. El primer par 11 es el par de los bits en la extrema derecha (101, 1001); el segundo par 00 es el siguiente par de bits (101, 1001); y así sucesivamente. Se amortigua la cadena de entrada con cuatro pares 00 —la longitud del número más grande 1001 que debe multiplicarse—. Como 101 ×1001 =101101, se asevera que se obtiene la salida mostrada en la tabla adyacente.

Soluciones Ejercicios Capítulo 11.5 Matemáticas Discretas Johnsonbaugh 6 ed
1. Demuestre que el conjunto de compuertas {OR, NOT} es funcionalmente completo. Demuestre que cada conjunto de compuertas en los ejercicios 2 al 5 no es funcionalmente completo.
2. {AND}
3. {OR}
4. {NOT}
5. {AND, OR}
6. Dibuje un circuito con sólo compuertas NAND que calcule xy.
7. Escriba xy usando sólo ↑.

Escriba expresiones booleanas para describir los circuitos de salidas múltiples en los ejercicios 9 al 11.



12. Diseñe circuitos usando sólo compuertas NAND para calcular las funciones de los ejercicios 1 al 10, sección 11.4.
13. ¿Puede reducir el número de compuertas NAND incluidas en cualquiera de los circuitos del ejercicio 12?
14. Diseñe circuitos que usen el menor número de compuertas AND, OR y NOT tanto como sea posible para calcular las funciones de los ejercicios 1 al 10, sección 11.4.
15. Diseñe un circuito medio sumador usando sólo compuertas NAND.
16. Diseñe un circuito medio sumador usando cinco compuertas NAND. Una compuerta NOR recibe entradas x1 y x2, donde x1 y x2 son bits, y produce una salida denotada por x1 ↓x2, donde

17. Escriba xy, x∨y, x y x ↑ y en términos de ↓.
18. Escriba x↓y en términos de ↑.
19. Escriba la tabla lógica para la función nor.
20. Demuestre que el conjunto de compuertas {NOR} es funcionalmente completo.
21. Diseñe circuitos usando sólo compuertas NOR para calcular las funciones de los ejercicios 1 al 10, sección 11.4.
22. ¿Puede reducir el número de compuertas NOR empleadas en cualquiera de sus circuitos para el ejercicio 21?
23. Diseñe un circuito medio sumador con sólo compuertas NOR.
24. Diseñe un circuito medio sumador con cinco compuertas NOR.
25. Diseñe un circuito con tres entradas que produce 1 justo cuando dos o tres entradas tienen valor 1.
26. Diseñe un circuito que multiplique los números binarios x2 x1 y y2 y1. La salida será de la forma z4 z3 z2 z1.
27. Un módulo de 2 es un circuito que acepta como entrada dos bits b y FLAGIN y produce bits c y FLAGOUT. Si FLAGIN = 1, entonces c=b y FLAGOUT =1. Si FLAGIN =0 y b=1, entonces FLAGOUT = 1. Si FLAGIN = 0 y b = 0, entonces FLAGOUT = 0. Si FLAGIN =0, entonces c=b. Diseñe un circuito para implementar el módulo de 2.
El complemento de 2 de un número binario se calcula utilizando el siguiente algoritmo.
Encuentre el complemento de 2 de los números en los ejercicios 28 al 30 usando el algoritmo 11.15.16.
28. 101100
29. 11011
30. 011010110
31. Utilizando módulos de 2, diseñe un circuito que calcule el complemento de 2 y3 y2 y1 del número binario de tres bits x3 x2 x1.
32. Sea *un operador binario en un conjunto S que contiene 0 y 1. Escriba un conjunto de axiomas para *, modelado tomando en cuenta las reglas que satisface NAND, de manera que si se define
entonces (S,∨,∧, , 0, 1) (S,∨,∧, , 0, 1) es un álgebra booleana.
33. Sea * un operador binario en S que contiene 0 y 1. Escriba un conjunto de axiomas para *, modelado tomando en cuenta las reglas que satisface NOR, y las definiciones de –, ∨ y ∧ de manera que sea un álgebra booleana.
34. Demuestre que {→} es funcionalmente completo (vea la definición 1.2.3).
35. Sea B(x, y) una expresión booleana en las variables x y y que sólo usa el operador ↔(vea la definición 1.2.8). a) Demuestre que si B contiene un número par de x, los valores de B( x , y) y B(x, y) son iguales para toda x y y. b) Demuestre que si B contiene un número impar de x, los valores de B( x , y) y B ( x . y ) son iguales para toda x y y. c) Utilice los incisos a) y b) para demostrar que {↔} no es funcionalmente completo. Paul Pluznikov contribuyó con este ejercicio.
2. {AND}
3. {OR}
4. {NOT}
5. {AND, OR}
6. Dibuje un circuito con sólo compuertas NAND que calcule xy.
7. Escriba xy usando sólo ↑.



12. Diseñe circuitos usando sólo compuertas NAND para calcular las funciones de los ejercicios 1 al 10, sección 11.4.
13. ¿Puede reducir el número de compuertas NAND incluidas en cualquiera de los circuitos del ejercicio 12?
14. Diseñe circuitos que usen el menor número de compuertas AND, OR y NOT tanto como sea posible para calcular las funciones de los ejercicios 1 al 10, sección 11.4.
15. Diseñe un circuito medio sumador usando sólo compuertas NAND.
16. Diseñe un circuito medio sumador usando cinco compuertas NAND. Una compuerta NOR recibe entradas x1 y x2, donde x1 y x2 son bits, y produce una salida denotada por x1 ↓x2, donde

17. Escriba xy, x∨y, x y x ↑ y en términos de ↓.
18. Escriba x↓y en términos de ↑.
19. Escriba la tabla lógica para la función nor.
20. Demuestre que el conjunto de compuertas {NOR} es funcionalmente completo.
21. Diseñe circuitos usando sólo compuertas NOR para calcular las funciones de los ejercicios 1 al 10, sección 11.4.
22. ¿Puede reducir el número de compuertas NOR empleadas en cualquiera de sus circuitos para el ejercicio 21?
23. Diseñe un circuito medio sumador con sólo compuertas NOR.
24. Diseñe un circuito medio sumador con cinco compuertas NOR.
25. Diseñe un circuito con tres entradas que produce 1 justo cuando dos o tres entradas tienen valor 1.
26. Diseñe un circuito que multiplique los números binarios x2 x1 y y2 y1. La salida será de la forma z4 z3 z2 z1.
27. Un módulo de 2 es un circuito que acepta como entrada dos bits b y FLAGIN y produce bits c y FLAGOUT. Si FLAGIN = 1, entonces c=b y FLAGOUT =1. Si FLAGIN =0 y b=1, entonces FLAGOUT = 1. Si FLAGIN = 0 y b = 0, entonces FLAGOUT = 0. Si FLAGIN =0, entonces c=b. Diseñe un circuito para implementar el módulo de 2.
El complemento de 2 de un número binario se calcula utilizando el siguiente algoritmo.
Encuentre el complemento de 2 de los números en los ejercicios 28 al 30 usando el algoritmo 11.15.16.
28. 101100
29. 11011
30. 011010110
31. Utilizando módulos de 2, diseñe un circuito que calcule el complemento de 2 y3 y2 y1 del número binario de tres bits x3 x2 x1.
32. Sea *un operador binario en un conjunto S que contiene 0 y 1. Escriba un conjunto de axiomas para *, modelado tomando en cuenta las reglas que satisface NAND, de manera que si se define

entonces (S,∨,∧, , 0, 1) (S,∨,∧, , 0, 1) es un álgebra booleana.
33. Sea * un operador binario en S que contiene 0 y 1. Escriba un conjunto de axiomas para *, modelado tomando en cuenta las reglas que satisface NOR, y las definiciones de –, ∨ y ∧ de manera que sea un álgebra booleana.
34. Demuestre que {→} es funcionalmente completo (vea la definición 1.2.3).
35. Sea B(x, y) una expresión booleana en las variables x y y que sólo usa el operador ↔(vea la definición 1.2.8). a) Demuestre que si B contiene un número par de x, los valores de B( x , y) y B(x, y) son iguales para toda x y y. b) Demuestre que si B contiene un número impar de x, los valores de B( x , y) y B ( x . y ) son iguales para toda x y y. c) Utilice los incisos a) y b) para demostrar que {↔} no es funcionalmente completo. Paul Pluznikov contribuyó con este ejercicio.
Suscribirse a:
Comentarios (Atom)